C/1935 Q1

Solar System
Dynamics &
Planetology
Group

C/1935 Q1 van Biesbroeck

General description

Comet C/1935 Q1 was discovered on 21 August 1935, about 7.5 months before perihelion passage, and soon a few prediscovery images were found (taken at Union Observatory in South Africa) extending arc to 3 July 1935; comet was last seen on 26 January 1938 [Kronk, Cometography: Volume 4].

This comet made two close approaches to the Earth, on 4 August 1935 (3.70 au) and on 6 August 1936 (3.62 au).

Solution given below is based on data span over 2.30 yr in a range of heliocentric distances from 4.83 au through perihelion (4.04 au) to 6.06 au.

Comet suffered small planetary perturbations during its passage through the planetary system, however they led to escape the comet from the planetary zone on a hiperbolic orbit (see future barycentric orbit given below).

More details in Królikowska et al. 2014, Królikowska and Dybczyński 2017

Figure caption: Time distribution of positional observations with corresponding heliocentric (red curve) and geocentric (green curve) distance at which they were taken. The horizontal dotted line shows the perihelion distance for a given comet whereas vertical dotted line — the moment of perihelion passage.

SSDP Cometary Note C1935Q1A5-001

Comet C/1935 Q1 van Biesbroeck

number of observations	131
number of residuals	250
data interval	1935 July 3 — 1937 Nov. 12
rms [arcsec]	1.49
orbit quality class	1a

Osculating orbital elements (heliocentric; ecliptic J2000.0)

Epoch (TT)	19360422.0	= JD 2428280.5
time of perihelion passage (TT)	19360511.635659	± 0.001683
perihelion distance	4.04341779	± 0.00000969
eccentricity	1.00206616	± 0.00002076
argument of perihelion [deg]	44.895725	± 0.000252
longitude of the ascending node [deg]	300.561472	± 0.000059
inclination [deg]	66.112186	± 0.000052
inverse semimajor axis [10^-6 au^-1]	-510.99	± 5.13

Note: Epoch is given in a format: yyyymmdd.d, time of perihelion passage in a format of yyyymmdd.dddddd.

Figure caption: Six 2D-projections of the 6D space of original swarm (5001 VCs) of C/1935 Q1. Each density map is given in logarithmic scale presented on the right in the individual panel.
The same figure in the new window

Original orbital elements (barycentric; at 250 au from the Sun)

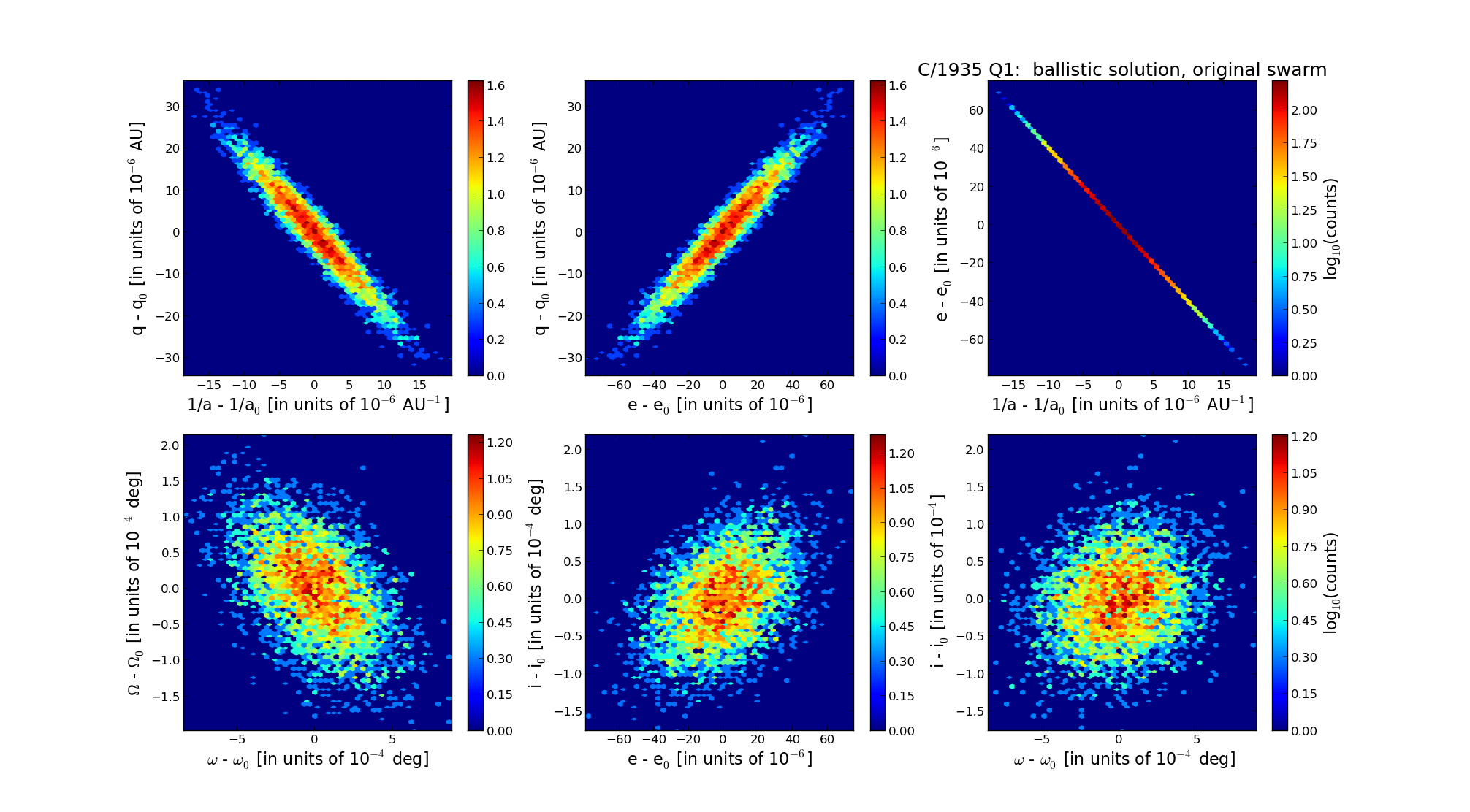
Epoch (TT)	16320922
time of perihelion passage (TT)	19360511.115435	± 0.001724
perihelion distance	4.03419814	± 0.00000988
eccentricity	0.99994692	± 0.00002095
argument of perihelion [deg]	45.035086	± 0.000250
longitude of the ascending node [deg]	300.599583	± 0.000060
inclination [deg]	66.129296	± 0.000051
inverse semimajor axis [10^-6 au^-1]	13.16	± 5.19

Note: Values of uncertainties of original/future orbital elements were derived using a swarm of 5001 osculating orbits of VCs (including the nominal osculating orbit given above) for original/future orbital evolution calclulations and then by fitting the distribution of a given orbital element of original/future swarm of VCs to Gaussian distribution.

Original barycentric positions and velocities of 5001 VCs at 250 au from the Sun are given here (data format), i.e. before entering the planetary zone.

Figure caption: Six 2D-projections of the 6D space of future swarm (5001 VCs) of C/1935 Q1. Each density map is given in logarithmic scale presented on the right in the individual panel.
The same figure in the new window

Future orbital elements (barycentric; at 250 au from the Sun)

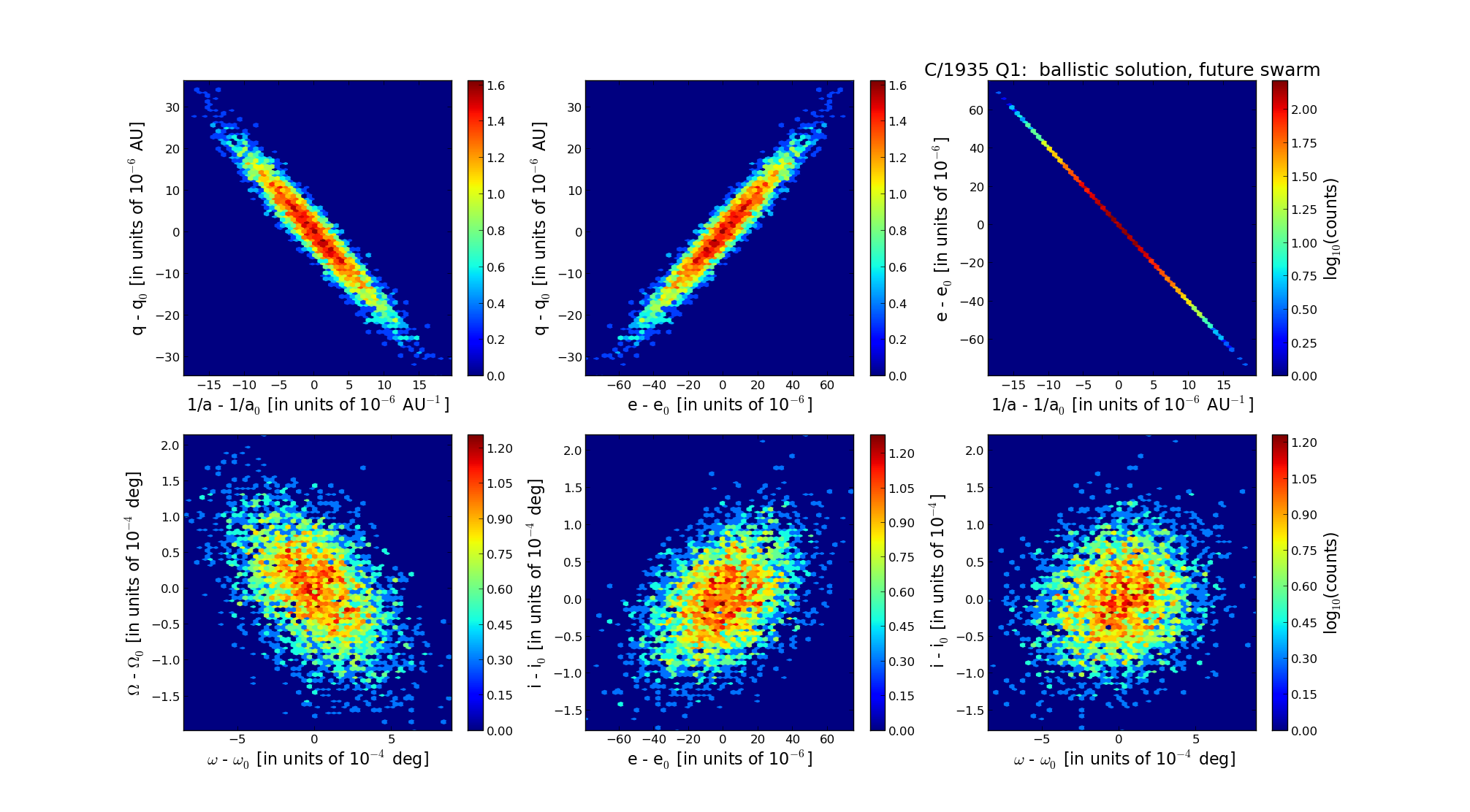
Epoch (TT)	22360807
time of perihelion passage (TT)	19360511.495408	± 0.001671
perihelion distance	4.03970045	± 0.00000994
eccentricity	1.00115405	± 0.00002096
argument of perihelion [deg]	44.839534	± 0.000252
longitude of the ascending node [deg]	300.607693	± 0.000060
inclination [deg]	66.119413	± 0.000051
inverse semimajor axis [10^-6 au^-1]	-285.68	± 5.19