C/1932 M2

Solar System
Dynamics &
Planetology
Group

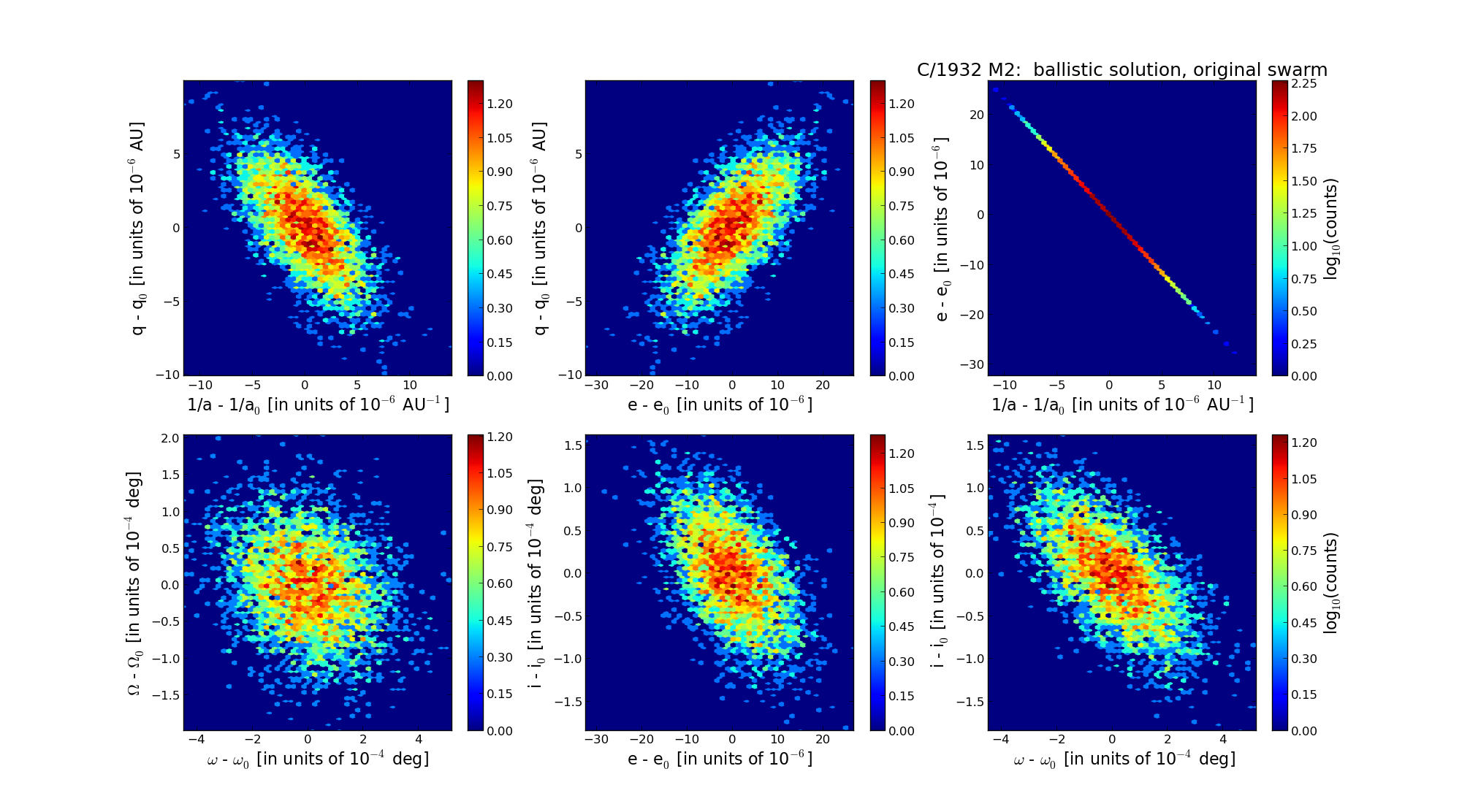
C/1932 M2 Geddes

General description

Comet C/1932 M2 was discovered on 22 June 1932, that is one month before perihelion passage, and was last seen on 19 July 1934 [Kronk, Cometography: Volume 3]. About year after discovery the prediscovery images on plates exposed on 14 August 1931 (at Bloemfontein, Harvard University Station in Soutk Africa) were found.

This comet made its closest approach to the Earth on 1 July 1932 (1.97 au), that is nine days after its discovery.

Solution given below is based on data span over 2.93 yr in a range of heliocentric distances from 4.78 au through perihelion (2.31 au) to 6.83 au.

Comet suffered small planetary perturbations during its passage through the planetary system, however they led to escape the comet from the planetary zone on a hiperbolic orbit (see future barycentric orbit given below).

This comet was in the original sample of 19 comets used by Oort for his hypothesis on LPCs.

More details in Królikowska et al. 2014

Figure caption: Time distribution of positional observations with corresponding heliocentric (red curve) and geocentric (green curve) distance at which they were taken. The horizontal dotted line shows the perihelion distance for a given comet whereas vertical dotted line — the moment of perihelion passage.

SSDP Cometary Note C1932M2A5-001

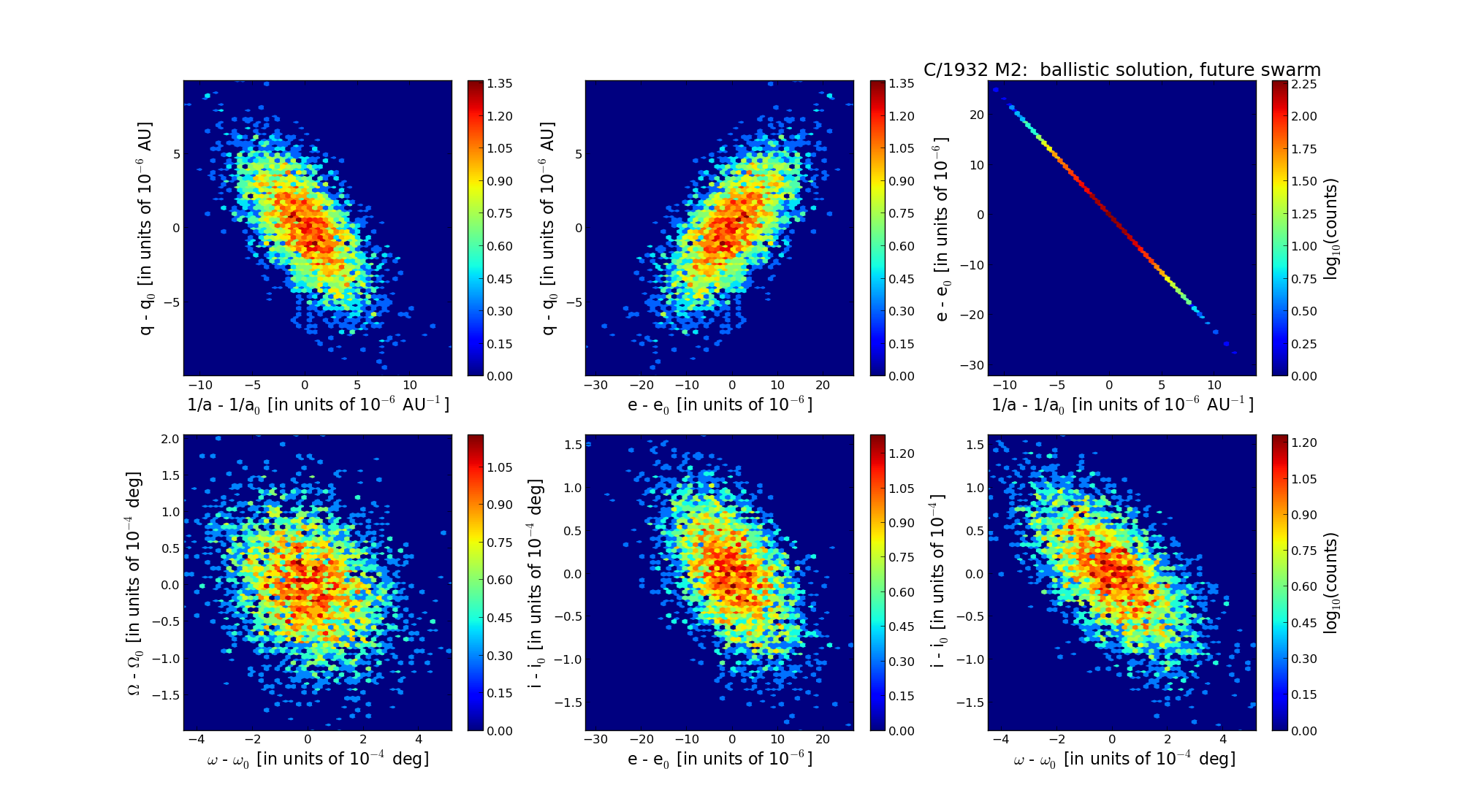
Comet C/1932 M2 Geddes

number of observations	329
number of residuals	546
data interval	1931 Aug. 14 — 1934 July 19
rms [arcsec]	1.77
orbit quality class	1a

Osculating orbital elements (heliocentric; ecliptic J2000.0)

Epoch (TT)	19320910.0	= JD 2426960.5
time of perihelion passage (TT)	19320921.074056	± 0.000474
perihelion distance	2.31356998	± 0.00000273
eccentricity	1.00140517	± 0.00000708
argument of perihelion [deg]	329.693866	± 0.000143
longitude of the ascending node [deg]	216.093463	± 0.000057
inclination [deg]	124.988856	± 0.000050
inverse semimajor axis [10^-6 au^-1]	-607.36	± 3.06

Note: Epoch is given in a format: yyyymmdd.d, time of perihelion passage in a format of yyyymmdd.dddddd.

Figure caption: Six 2D-projections of the 6D space of original swarm (5001 VCs) of C/1932 M2. Each density map is given in logarithmic scale presented on the right in the individual panel.
The same figure in the new window

Original orbital elements (barycentric; at 250 au from the Sun)

Epoch (TT)	16310819
time of perihelion passage (TT)	19320921.542393	± 0.000469
perihelion distance	2.31250621	± 0.00000275
eccentricity	0.99986916	± 0.00000710
argument of perihelion [deg]	329.793942	± 0.000144
longitude of the ascending node [deg]	216.089015	± 0.000057
inclination [deg]	125.023427	± 0.000050
inverse semimajor axis [10^-6 au^-1]	56.58	± 3.07

Note: Values of uncertainties of original/future orbital elements were derived using a swarm of 5001 osculating orbits of VCs (including the nominal osculating orbit given above) for original/future orbital evolution calclulations and then by fitting the distribution of a given orbital element of original/future swarm of VCs to Gaussian distribution.

Original barycentric positions and velocities of 5001 VCs at 250 au from the Sun are given here (data format), i.e. before entering the planetary zone.

Figure caption: Six 2D-projections of the 6D space of future swarm (5001 VCs) of C/1932 M2. Each density map is given in logarithmic scale presented on the right in the individual panel.
The same figure in the new window

Future orbital elements (barycentric; at 250 au from the Sun)

Epoch (TT)	22300730
time of perihelion passage (TT)	19320921.652251	± 0.000480
perihelion distance	2.30775841	± 0.00000273
eccentricity	1.00052850	± 0.00000709
argument of perihelion [deg]	329.645277	± 0.000144
longitude of the ascending node [deg]	216.182491	± 0.000058
inclination [deg]	125.017993	± 0.000050
inverse semimajor axis [10^-6 au^-1]	-229.01	± 3.07